List of Prime Numbers from 1 to 100

Prime numbers have fascinated mathematicians for centuries. A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. In other words, it is a number that can only be divided by 1 and itself. In this article, we will explore the list of prime numbers from 1 to 100, their properties, and some interesting facts about them.

What is Prime Number?

A prime number is a fundamental concept in mathematics. A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. In other words, a prime number can only be divided evenly by 1 and itself.

For example, the first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and so on. These numbers are considered prime because they cannot be divided evenly by any other numbers except for 1 and themselves.

The List of Prime Numbers from 1 to 100

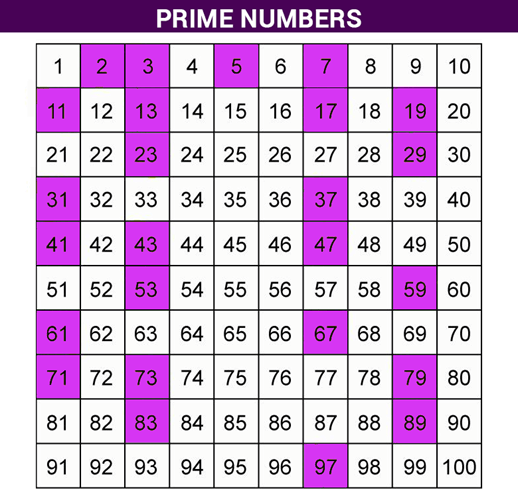
List of the prime numbers from 1 to 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.

There are 25 prime numbers from 1 to 100. Note that 1 is not a prime number because it has only one divisor, which is itself.

Prime Numbers Graph up to 100

How to calculate a number is Prime?

To calculate whether a given number is prime, you can use one of the methods I mentioned earlier, such as the trial division method or the Sieve of Eratosthenes method. Here are the basic steps for each method:

• Trial division method:
  • Start with the number n you want to check for primality.
  • Test whether n is divisible by any number from 2 to the square root of n.
  • If n is divisible by any of these numbers, then it is not a prime number.
  • If n is not divisible by any of these numbers, then it is a prime number.
• Sieve of Eratosthenes method:
  • Create a list of all numbers from 2 to n.
  • Starting with 2, cross out all multiples of 2 in the list.
  • Move to the next uncrossed number, which should be 3, and cross out all multiples of 3.
  • Continue this process, crossing out multiples of all remaining uncrossed numbers up to the square root of n.
  • If n is not crossed out, then it is a prime number.

Properties of Prime Numbers

Prime numbers have some interesting properties that make them unique. Here are some of the most notable properties:

• Prime numbers are only divisible by 1 and themselves.
• The sum of any two prime numbers is always an even number, except when one of the primes is 2.
• The product of any two prime numbers is always a composite number.
• There are an infinite number of prime numbers.

FAQs